The kappa coefficient of agreement

Author

Šimon Kucharský

Published

May 6, 2025

Code

import os
if "KERAS_BACKEND" not in os.environ:
    # set this to "torch", "tensorflow", or "jax"
    os.environ["KERAS_BACKEND"] = "jax"

import numpy as np
import bayesflow as bf
import matplotlib.pyplot as plt

\[\begin{equation} \begin{aligned} \alpha, \beta, \gamma & \sim \text{Beta}(1, 1)\\[1pt] \pi_a & \leftarrow \alpha \beta \\ \pi_b & \leftarrow \alpha (1-\beta) \\ \pi_c & \leftarrow (1-\alpha) (1-\gamma) \\ \pi_d & \leftarrow (1-\alpha) \gamma \\ \epsilon & \leftarrow \alpha\beta + (1-\alpha)\gamma\\ \psi & (\pi_a + \pi_b) (\pi_a + \pi_c) + (\pi_b + \pi_d) (\pi_c + \pi_d) \\ \kappa & \leftarrow (\epsilon - \psi) / (1-\psi)\\[1pt] y & \sim \text{Multinomial}(\pi, n) \end{aligned} \end{equation}\]

Simulator

Code

def context():
    return dict(n=np.random.randint(low=150, high=600))

def prior():
    alpha = np.random.beta(a=1, b=1)
    beta  = np.random.beta(a=1, b=1)
    gamma = np.random.beta(a=1, b=1)

    pi = np.array([
        alpha * beta,
        alpha * (1-beta),
        (1-alpha) * (1-gamma),
        (1-alpha) * gamma
    ])

    epsilon = alpha * beta + (1-alpha) * gamma
    psi = (pi[0] + pi[1]) * (pi[0] + pi[2]) + (pi[1] + pi[3]) * (pi[2] + pi[3])
    
    kappa = (epsilon - psi)/(1-psi)

    return dict(pi=pi, kappa=kappa)

def likelihood(n, pi):
    y = np.random.multinomial(n=n, pvals=pi)
    return dict(y=y)

simulator = bf.make_simulator([context, prior, likelihood])

Approximator

Code

adapter = (
    bf.Adapter()
    .constrain("kappa", lower=-1, upper=1)
    .rename("kappa", "inference_variables")
    .rename("y", "inference_conditions")
)

Code

workflow = bf.BasicWorkflow(
    simulator=simulator,
    adapter=adapter,
    inference_network=bf.networks.CouplingFlow()
)

Training

Code

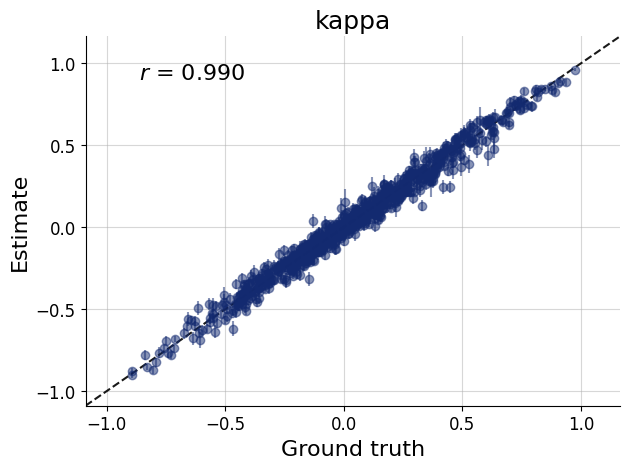
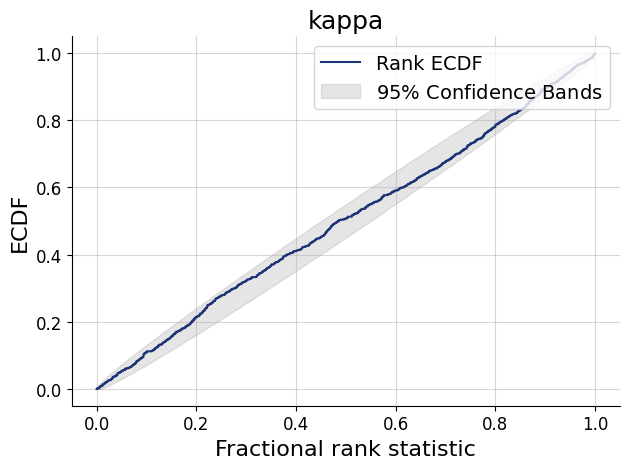
history = workflow.fit_online(epochs=50, batch_size=512)

Validation

Code

test_data = simulator.sample(1000)
figs=workflow.plot_default_diagnostics(test_data=test_data, num_samples=500)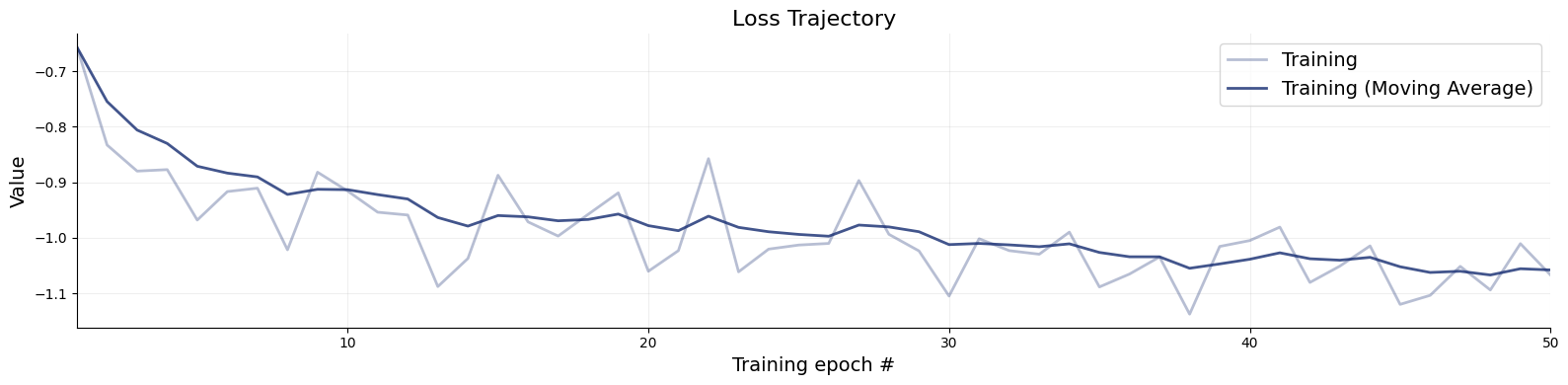

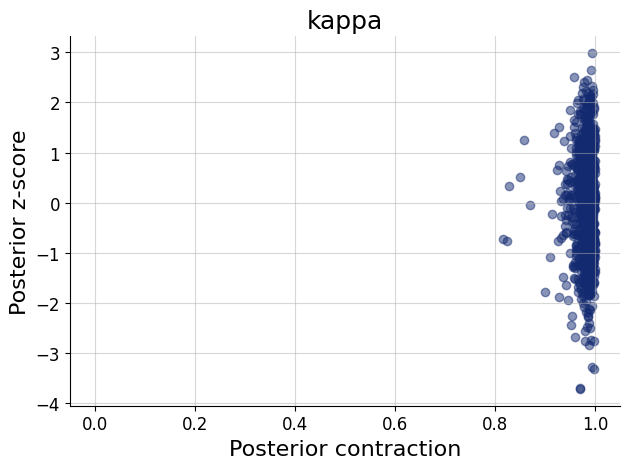
Inference

We will apply the model to three datasets reported by Lee & Wagenmakers (2013, pp. 67–68).

Code

inference_data = dict(
    y = np.array(
        [
            [14, 4, 5, 210], # influenza
            [20, 7, 103, 417], # hearing loss
            [0, 0, 13, 157], # rare disease
        ]
    )
)

Code

samples = workflow.sample(num_samples=2000, conditions=inference_data)

Code

fig, axs = plt.subplots(ncols=3)
titles = ["Influenza", "Hearing loss", "Rare Disease"]

for i, ax in enumerate(axs):
    ax.set_title(titles[i])
    ax.hist(samples["kappa"][i], 
            density=True, color="lightgray", edgecolor="black", bins=np.arange(-1, 1.05, 0.05))

fig.supxlabel(r"$\kappa$")
fig.supylabel("Density")
fig.tight_layout()

References

Lee, M. D., & Wagenmakers, E.-J. (2013). Bayesian Cognitive Modeling: A Practical Course. Cambridge University Press.

Reuse

CC BY NC